Karol Gauss - Olga Bakun

Karol Fryderyk Gauss, nazywany przez swoich współczesnych Księciem Matematyków, pochodził z rodu zgoła nieksiążęcego i nie mającego ani tradycji, ani pretensji do - podstawowego nawet - wykształcenia. Ojciec Karola był pomocnikiem murarskim i swojego syna początkowo przeznaczał do podobnej kariery. Na szczęście niepospolity talent młodziutkiego Gaussa objawił się na tyle wcześnie i w sposób tak ewidentny, że znalazł się oświecony i możny sponsor, dzięki któremu matematyka nie straciła jednego ze swoich najwybitniejszych mężów. Większość z nas zna zapewne prawdziwą anegdotkę o siedmioletnim Gaussie i jego nieco sadystycznym nauczycielu matematyki, który kazał swoim małoletnim (8-9?) uczniom obliczyć sumę liczb od 1 do 100. Karolek po pięciu minutach przedstawił kartkę z rzeczywiście króciutkim wywodem:

1	2	...	49	50
100	99	...	52	51
101	101	...	101	101

Nauczyciel, (choć bez fantazji) był człowiekiem porządnym i po dwóch latach nauki wziął młodego matematyka pod rękę i zaprowadził do księcia Brunszwiku, Ferdynanda. Ten, usłyszawszy, że Karolek już umie lepiej matematykę od swojego nauczyciela, zgodził się na finansowanie dalszej nauki. Po kilku latach w Collegium Carolinum (gimnazjum), 18-letni Gauss rozpoczął studia na uniwersytecie w Getyndze (Göttingen).

Jeszcze jako uczeń gimnazjum Gauss sformułował metodę najmniejszych kwadratów (drugim - niezależnym - jej twórcą był Adrien-Marie Legendre, ten od naszych ukochanych wielomianów Legendre'a i innych ciekawych matematycznych figlików).

Być może Gauss, młody człowiek o wybitnym, "ścisłym" umyśle, wybrałby inny zawód niż matematyka - posiadał on wybitne uzdolnienia językowe i rozważał dalsze studia języków klasycznych - gdyby nie drobny przypadek. W 1796 udało mu się udowodnić, że jest możliwa konstrukcja foremnego 17-kąta przy użyciu tzw. narzędzi Euklidesa, to znaczy cyrkla i linijki. Starożytni Grecy znali oczywiście takie foremne wielokąty jak trójkąt równoboczny, kwadrat, pięciokąt i piętnastokąt, a także "parzyste" wielokąty, powstające przez podwojenie liczby boków w wyżej wymienionych: sześciokąt, ośmiokąt, itd. Trójkąt i kwadrat to sprawy oczywiste, pięciokąt już nieco mniej. Konstrukcja kąta 72^o (lub 36^o) wymaga nieco pomyślunku - ale można ją znaleźć już u Euklidesa. Wiąże się ona zresztą z problemem złotego podziału odcinka o długości a: większa część odcinka, x, ma się do mniejszej w tym samym stosunku, w jakim ma się do niej samej cały odcinek; algebraiczne jego sformułowanie to

W wydanych w 1801 Disquisitiones Arithmeticae Gauss wykazał, że regularny p-kąt, gdzie p jest liczbą pierwszą, można skonstruować narzędziami Euklidesowymi, pod warunkiem, że p ma postać

Takimi liczbami pierwszymi, dla k = 0,1,2,3,4 są p = 3, 5, 17, 257 i 65 367. Dla k=5 liczba 2³²+1 jest podzielna przez 641 (pierwszy wykazał to Euler). Potem liczby typu 1 już nie są pierwsze - to znaczy, dla kolejnych k można to sprawdzić, ale ...nikt tego nie udowodnił dla wszystkich k (Gauss nie zdążył ?). Gauss był tak dumny ze swego wyczynu, że prosił nawet pod koniec życia, aby regularny 17-kąt znalazł się - zamiast epitafium - na jego nagrobku. Kamieniarz nie podjął się jednak tego zadania - taki ,,wielokąt'' nie różni się zbytnio od koła. Za to wdzięczni rodacy Gaussa umieścili, na piedestale jego pomnika, 17-ramienną gwiazdę.

Jednym z pierwszych i najbardziej głośnych tryumfów Gaussa był związany z odkryciem (podczas pierwszej nocy 19. Wieku, 1 stycznia 1801) planetoidy Ceres, przez włoskiego astronoma Piazzi'ego. Astronom obserwował planetoidę, (która zapoczątkowała tę nową kategorię obiektów nieba) przez 6 tygodni, w ciągu których Ceres przebiegła raptem 9^o łuku. Potem znalazła się blisko Słońca - i skończyły się obserwacje. Z danych Prazziego Gauss wyliczył orbitę Ceres z taką dokładnością, że po upływie roku astronomowie nie mieli najmniejszych trudności z ponownym zarejestrowaniem jej w miejscu, którego współrzędne wynikały z rachunku! Ten tryumf na swój sposób źle się przysłużył matematyce - Gauss przez 20 lat z pasją rachował orbity kolejno odkrywanych planetoid: Pallas, Juno i Westy. Wyniki opisał w swoim znakomitym Theoria Motus Corporum Coelestium in Sectionibus Conicus Solem Ambietium (Teoria ciał niebieskich obiegających Słońce po orbitach stożkowych). Książka ta, eksponująca między innymi potęgę metody najmniejszych kwadratów, stała się biblią 19-wiecznych astronomów. W latach 1845-1846 obserwacje ,,zakłóceń '' orbity niedawno (1781) odkrytego Urana doprowadziły do zapostulowania w określonym miejscu nowej planety - Neptuna. Odkrycia tego dokonali niezależnie Anglik Adams i Francuz Leverrier, chociaż - głównie za sprawą niechlujstwa angielskiego Astronoma Królewskiego, który nie bardzo dawał wiary ,,teoretycznym'' wymysłom młodego i mało znanego w kręgach astronomów Adamsa, chwała przypadła Francuzom.

Prawdziwą klęską dla Gaussa okazała się kampania napoleońska. W bitwie pod Jeną (1806) poległ książę Brunszwiku, główny dowódca pruskich wojsk. Gauss stracił sponsora i zaczął rozglądać się za posadą. Kusząca propozycja czekała (od czasu historii z Ceres) z Petersburskiej Akademii, ale przyjaciele z uniwersytetu Getyngi zaproponowali mu stanowisko dyrektora nowoutworzonego obserwatorium astronomicznego. Gauss chętnie się zgodził i do końca życia pozostał w Getyndze.

Nie był to jednak koniec napoleońskich awantur. W 1807, z zagarniętych przez Napoleona ziem niemieckich utworzono buforowe królestwo Westfalii. Królem został (oczywiście!) najmłodszy braciszek cesarza. A ponieważ wojny trwały, pieniędzy było mało nowy król nałożył na niemiecką ludność kontrybucję. Na Gaussa przypadło dwa tysiące franków - suma ogromna na ówczesne czasy, a także na możliwości uniwersyteckiego profesora (uniwersytet płacił w ogóle kiepsko, a z powodu wojen - nieregularnie). Ładny gest wykonał wówczas Laplace, opłacając za Gaussa kontrybucję i powiadamiając o tym Gaussa w pełnym szacunku liście. Jednakże Gauss miał swój honor - skrupulatnie spłacił, w ciągu kilku lat, wyłożoną za niego sumę wraz z odsetkami i do końca życia nie lubił Francji.

Gaussa teoria liczb - kongruencja, czyli przystawanie

Jeżeli nawet Gauss nie był autorem tego powiedzenia, to było ono z pewnością mottem numer 1. (Były i inne) jego twórczego życia. Teoria liczb fascynowała i fascynuje matematyków od najdawniejszych czasów. Mistyczne skojarzenia Pitagorejczyków, zażarte poszukiwania liczb doskonałych (ojciec Mersenne), małe i wielkie twierdzenie Fermat'a - to tylko kilka z nieprzebranej różnorodności problemów. Teoria liczb jest na swój sposób łatwa i trudna: łatwa, bo można do niej,,wystartować'' bez specjalnego przygotowanie formalnego, trudna - bo niektóre oczywiste (?) Przypuszczenia opierają się przez setki lat rygorystycznym dowodom. Niekiedy rzeczy ,,trudne'' stają się dziecinnie łatwe - jeżeli tylko pojawi się sprytna metoda uwidaczniania (i udowadniania) pewnych własności. Taką metodą jest właśnie teoria kongruencji, albo przystawania liczb. Nie jest ona wyłącznie dziełem Gaussa, ale została przez niego dopracowana, skodyfikowana i...wykorzystana do rozstrzygnięcia wielu pytań związanych z podzielnością liczb.

Definicja:
Niech n będzie dodatnią liczbą całkowitą, natomiast a i b - dowolnymi liczbami (całkowitymi - rozmawiamy wyłącznie o liczbach całkowitych). Liczby a i b nazywamy przystającymi (kongruentnymi) modulo n i piszemy

$\begin{displaymath}a - b = kn, \;\;\; (k \mbox{\rm -- całkowite}).\end{displaymath}$

$\begin{displaymath}3 \equiv 23 \mbox{\rm (mod } 7); \;\;\; -31 \equiv 11 \mbox{\rm (mod } 7);\;\;\; -15 \equiv -64 \mbox{\rm (mod } 7), \end{displaymath}$

$\begin{displaymath}3 -24 = 21 = 3\cdot 7; \;\;\; -31-11 = -42 = -6\cdot 7; \;\;\; -15-(-64) = 49 = 7\cdot 7. \end{displaymath}$

Analogicznie, możemy mówić o liczbach, które nie są przystające modulo n i pisać

Na przykład: $25\not\equiv 12 \mbox{\rm (mod } 7)$ , bo 25-12 = 13 - liczbie, która nie jest podzielna przez 7. Z definicji natychmiast wynika oczywiste twierdzenie: warunkiem koniecznym i wystarczającym, aby $a \equiv b \mbox{\rm (mod } n)$ jest, aby reszty z dzielenia a i b przez n były równe. Dowód (w obie strony)jest prosty. Na przykład:

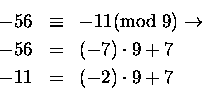
$\begin{eqnarray*}-56 & \equiv & -11 \mbox{\rm (mod } 9) \rightarrow \\ -56 & = & (-7)\cdot 9 + 7 \\ -11 & = & (-2)\cdot 9 + 7 \end{eqnarray*}$

- reszta w obu przypadkach wynosi 7. Kongruencja albo (po polsku) przystawanie liczb całkowitych okazuje się mieć podobne własności w stosunku do operacji dodawania, mnożenia i potęgowania jak zwykła relacja równości. Podstawowe własności kongruencji to:

$\{ a \equiv b \mbox{\rm (mod } n) \mbox{\rm i } b \equiv c \mbox{\rm (mod } n)\} \rightarrow a \equiv c \mbox{\rm (mod } n)$ ;

$\{ a \equiv b \mbox{\rm (mod } n) \mbox{\rm i } c \equiv d \mbox{\rm (mod } n)\}$
$\rightarrow a + c \equiv b+ d \mbox{\rm (mod } n) \mbox{\rm oraz } a \cdot c \equiv b\cdot d \mbox{\rm (mod } n)$

$a \equiv b \mbox{\rm (mod } n) \rightarrow \{ a + c \equiv b+ c \mbox{\rm (mod } n) \mbox{\rm oraz } a \cdot c \equiv b\cdot c \mbox{\rm (mod } n) \}$ ;

Jean Pierre Fermat miał pomysł (jeden z wielu !), że wszystkie liczby o postaci 2^2k +1 są liczbami pierwszymi (pamiętasz, dla liczb p naprawdę pierwszych o tej postaci, Gauss udowodnił możliwość ,,Euklidesowej'' konstrukcji regularnego p -kąta). Dla k=0,1,2,3 i 4 wszystko jest prawdziwe, ale już Euler (ca. 1735) zauważył, że 2²⁵ +1 dzieli się przez 641. Wykazanie tego, korzystając z kongruencji, jest szybkie, łatwe i przyjemne. W języku ,,przystawania'' mamy wykazać, że:

$\begin{displaymath}2^{2^5} +1 = 2^{32} +1 \equiv 0 \mbox{\rm (mod } 641) .\end{displaymath}$

W tym celu musimy w liczbie 641 doszukać się podobnej struktury, jak w 2³² + 1. Dość oczywisty pomysł (ważne są potęgi dwójki!), to:

$\begin{displaymath}641 = 640 +1 = 5\cdot 128 +1 = 5\cdot 2^7 + 1.\end{displaymath}$

$\begin{displaymath}5\cdot 2^7 \equiv -1 \mbox{\rm (mod } 641).\end{displaymath}$

$\begin{displaymath}5^4\cdot (2^7)^4 \equiv (-1)^4 \mbox{\rm (mod } 641) \mbox{\rm albo}\end{displaymath}$

$\begin{displaymath}5^4\cdot 2^{28} \equiv 1 \mbox{\rm (mod } 641).\end{displaymath}$

W naszej 2²⁵ +1 mamy jednak tylko potęgę (32-gą) dwójki, a nie uświadczysz w niej potęgi piątki. Musimy znaleźć jakąś kongruencją (modulo 641) która zachodzi między potęgami dwójki i piątki. Każdy widzi, że 5⁴ to 625, które odległe jest od 641 o 16 = 2⁴:

$\begin{displaymath}5^4 \equiv -16 = -(2^4)\mbox{\rm (mod } 641).\end{displaymath}$

Możemy wykazać, że nie jest możliwa euklidesowa konstrukcja 2²⁵ +1-kąta foremnego:

$\begin{displaymath}2^{32} +1 = 2^{4}\cdot 2^{28} +1 \equiv -(5^4)\cdot 2^{28} +1 \equiv -1 + 1 = 0 \mbox{\rm (modulo } 641). \end{displaymath}$

liczba Mersenne'a 2⁸³ - 1 (postulowana przez swojego patrona jako kandydatka na liczbę pierwszą) dzieli się przez 167 (to też pokazał Euler). Tutaj dwójka występuję w potędze przeszło dwa i pół raza większej niż w poprzednim przykładzie. Trzeba podnieść do kwadratu i szukać partnerów kongruentnych (modulo 167) dla kolejnych potęg:

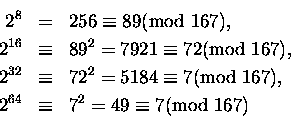
$\begin{eqnarray*}2^8 & = & 256 \equiv 89 \mbox{\rm (mod } 167), \\ 2^{16} & \e... ...\\ 2^{64} & \equiv & 7^2 = 49 \equiv 7 \mbox{\rm (mod } 167) \end{eqnarray*}$

Teraz tylko pozostało rozpisanie 83-ej potęgi dwójki. 83 = 16 + 67. A 67 nie jest dalekie od 64:

$\begin{displaymath}2^{67} = 2^3\cdot 2^{64} \equiv 8\cdot 49\mbox{\rm (mod } 167) = 392 \mbox{\rm (mod } 167) \equiv 58 \mbox{\rm (mod } 167).\end{displaymath}$

$\begin{displaymath}2^{83} - 1 = 2^{67}\cdot 2^{16} - 1 \equiv 58\cdot 72 \mbox{\... ...od } 167) -1 = 4167 -1 = 4166 \equiv 0 \mbox{\rm (mod } 167).\end{displaymath}$

a²	$\textstyle \equiv$	$\displaystyle 0 \mbox{\rm lub } 1 \mbox{\rm (mod 3)}$	(2)
a³	$\textstyle \equiv$	$\displaystyle 0 \mbox{\rm lub } 1 \mbox{\rm lub } -1 \mbox{\rm (mod 7)}$	(3)
a⁴	$\textstyle \equiv$	$\displaystyle 0 \mbox{\rm lub } 1 \mbox{\rm (mod 5)}$	(4)

Gaussa teoria liczb - dowody twierdzeń

$a \equiv b \mbox{\rm (mod } n) \rightarrow a-b = kn \rightarrow b-a = -kn \rightarrow b \equiv a \mbox{\rm (mod } n)$

$\{ a \equiv b \mbox{\rm (mod } n) \mbox{\rm i } b \equiv c \mbox{\rm (mod } n)\} \rightarrow \{a-b = hn \mbox{\rm oraz } c - d = gn\}$ a więc $a - c = (h+g) n \rightarrow a \equiv c \mbox{\rm (mod } n)$ ;

$\{ a \equiv b \mbox{\rm (mod } n) \mbox{\rm i } c \equiv d \mbox{\rm (mod } n)\} \rightarrow \{a-b = hn \mbox{\rm oraz } c - d = gn\}$
$(a+c) - (b+d) = (a-b) + (c-d) = (h+g) n \rightarrow a + c \equiv b+ d \mbox{\rm (mod } n)$
dla $a \cdot c \equiv b\cdot d \mbox{\rm (mod } n)$ dowód analogiczny.

$a \equiv b \mbox{\rm (mod } n) \rightarrow$
$a + c \equiv b+ c \mbox{\rm (mod } n) \mbox{\rm oraz } a \cdot c \equiv b\cdot c \mbox{\rm (mod } n)$ ;
dowód jak (4) z uwzględnieniem (1) - $c \equiv c \mbox{\rm (mod } n)$

$a \equiv b \mbox{\rm (mod } n) \rightarrow a^{k+1} \equiv b^{k+1} \mbox{\rm (mod } n)$
Dowód indukcyjny. Teza spełniona jest dla k=1. Zakładamy jej prawdziwość dla pewnego k. Mamy, więc:

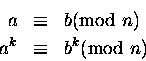
$\begin{eqnarray*}a &\equiv& b \mbox{\rm (mod } n)\\ a^k &\equiv& b^k \mbox{\rm (mod } n) \end{eqnarray*}$

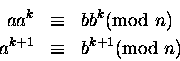
$\begin{eqnarray*}aa^k &\equiv& bb^k \mbox{\rm (mod } n)\\ a^{k+1} &\equiv& b^{k+1} \mbox{\rm (mod } n) \end{eqnarray*}$

Dowód twierdzenia o takiej samej reszcie (r): $a\equiv b \mbox{\rm (mod } n) \rightarrow a = kb + n = \ldots$
przy dzieleniu b przez n zostaje reszta r; tak więc b = qn +r
$\ldots = (qn + r) + kn = (q+k)n r \rightarrow$ - przy dzieleniu a przez n zostanie też reszta r. W drugą stronę - reszty takie same: a = q₁n +r i b = q₂ n + r. odejmując stronami $a-b = (q_1 - q_2) n \rightarrow a \equiv b \mbox{\rm (mod } n).$

Po roku 1820) Gauss zajął się geodezją: zagadnieniami związanymi z matematycznym określeniem kształtu i rozmiarów Ziemi. Aby zwiększyć dokładność danych Gauss opracował nowy przyrząd - heliotrop, wykorzystujący (jak sama nazwa wskazuje) promienie Słońca do pomiaru krzywizny powierzchni. Właśnie przy okazji studiów geodezyjnych ujrzała światło dzienne słynna krzywa rozkładu normalnego (Gaussa) błędów.

Ponieważ teorie geodezyjne były wówczas jeszcze w powijakach G. opracował sam teorię zakrzywionych powierzchni, dzięki której szczegółowy opis danej powierzchni mógł zostać wydedukowany z pomiarów długości krzywych leżących na tej powierzchni. Teoria ta znalazła godnego kontynuatora w osobie Bernarda Riemanna, który rozwinął teorię zakrzywionych powierzchni na 3- i wielo-wymiarową geometrię przestrzenną. Teoria Riemanna ujrzała światło dzienne tuż przed śmiercią Gaussa - w 60 lat później stała się punktem wyjścia dla ogólnej teorii względności Einsteina!

Gauss jako jeden z pierwszych poddał w wątpliwość wewnętrzną spójność euklidesowej geometrii. Gdy w latach 1830-ych Janosz Bolyai (Węgier) i Mikołaj Łobaczewski (Rosjanin) opublikowali niezależnie swoje prace o nie-euklidesowej geometrii, Gauss wyciągnął bardzo podobne wyniki, uzyskane 30 lat wcześniej. Trzeba tu zaznaczyć, że Gauss był z jednej strony niesłychanie twórczym umysłem, a z drugiej - rygorystycznym pedantem. Często uzyskane wyniki pozostawały na dnie szuflady, bo zainteresowanie uczonego przenosiło się już gdzie indziej, a publikowanie ,,niedopracowanych'' teorii nie wchodziło w rachubę. Dewizy Gaussa brzmiały "Pauca, sed matura" ("Skromnie, ale dojrzale") oraz "Ut nihil amplius desiderandum relictum sit" ("Aby nic więcej nie pozostawało do zrobienia").

Fizyka I tutaj nazwisko Gaussa pojawia się i to częściej niż myślimy. Oczywiście pierwsze skojarzenie to prawo Gaussa w elektrostatyce. Prace Gaussa nad teorią potencjału stanowią znaczne rozszerzenie prawa Coulomba - połączenie idei siły (natężenia pola) zmieniającej się odwrotnie proporcjonalnie do kwadratu odległości ze stałością strumienia wektora tej siły, obliczonego dla zamkniętej powierzchni i z wartością całkowitego ładunku zamkniętego wewnątrz powierzchni stanowiło tour de force ówczesnej fizyki. Twierdzenie Gaussa to perła analizy wektorowej - nieocenione w opisie wektorowych pól fizycznych.

W 1841 Gauss opublikował swoją Teorię optyki, w której rzeczywiście położył podwaliny pod dział optyki nazywany optyką geometryczną. To właściwie jemu zawdzięczamy takie pojęcie jak oś optyczna, odległość ogniskowa, ognisko i środek soczewki.

Wreszcie - każdy wie, że jednostką natężenia pola magnetycznego w starym, układzie cgs jest 1 Gauss. W latach 40-tych 19. Wieku Gauss współpracował z niemieckim fizykiem Wilhelmem Weberem. Razem prowadzili badania magnetyzmu ziemskiego, inspirując innych fizyków (praktycznie z całego świata) do podobnych pomiarów, prowadzonych w skoordynowany i regularny sposób. Wyniki Webera i Gaussa zostały wykorzystane przez twórców pierwszego telegrafu. Tak naprawdę to obaj panowie zbudowali pierwszy elektryczny telegraf, ale pomysł, że ten przyrząd mógłby stać się zalążkiem ,,światowego'' systemu komunikacji nie przypadł Gaussowi do gustu.

A jeszcze były prace nad teorią cieczy, włoskowatością i napięciem powierzchniowym. Nie tylko nowe i ciekawe tematy, ale rozwiązywane w nowoczesny i dojrzały sposób - z podkreśleniem roli prawa zachowania energii i (pierwszymi!) zastosowaniami rachunku wariacyjnego.

Parę słów warto powiedzieć o Gaussie jako ,,zwykłym'' człowieku. Był dwukrotnie żonaty - pierwsza żona umarła po czterech latach małżeństwa, wkrótce po urodzeniu ich trzeciego dziecka. Także i druga żona urodziła Gaussowi trójkę dzieci. Dwóch synów wyemigrowało do Ameryki.

Opisane na początku problemy finansowe Gaussa, wynikłe z napoleońskiej kontrybucji, wyszły mu na korzyść. Ocenia się, że umierając pozostawił majątek, którego wartość była przynajmniej stokrotną wielokrotnością jego aktualnych, rocznych zarobków. A warto wspomnieć, że w ciągu swego życia zgromadził Gauss pokaźną bibliotekę - ponad 6 tysięcy książek. Były wśród nich książki pisane w ,,interlingua hominorum scientiae'' - języku ludzi nauki - czyli łacinie. Były dzieła w klasycznej grece, a także książki angielskie francuskie, duńskie i - oczywiście - niemieckie.

Carl Friedrich Gauss - Princeps mathematicorum

Gaussa teoria liczb - kongruencja, czyli przystawanie

Gaussa teoria liczb - dowody twierdzeń